Overview

Relating Reaction Mechanisms

In a multistep reaction mechanism, one of the elementary steps progresses significantly slower than the others. This slowest step is called the rate-limiting step (or rate-determining step). A reaction cannot proceed faster than its slowest step, and hence, the rate-determining step limits the overall reaction rate.

The concept of rate-determining step can be understood from the analogy of a 4-lane freeway with a short-stretch of traffic-bottleneck caused due to lane-closure. Like the bottleneck affecting the overall rate at which vehicles could travel, the slowest elementary step influences the net reaction rate.

Rate laws may be derived directly from the balanced chemical equations for elementary reactions. However, this is not the case for most chemical reactions, where balanced equations often represent the overall change in the chemical system, resulting from multistep reaction mechanisms. Therefore, the rate law must be determined from experimental data, and the reaction mechanism subsequently deduced from the rate law.

For instance, consider the reaction of NO₂ and CO:

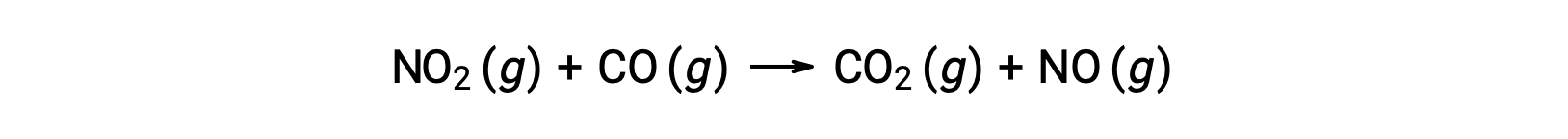
The experimental rate law for this reaction at temperatures above 225 °C is:

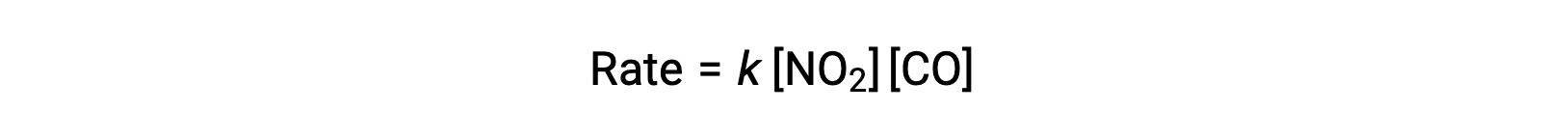
According to the rate law, the reaction is first order with respect to NO₂ and first-order with respect to CO. This is consistent with a single-step bimolecular mechanism, and it is possible that this reaction mechanism is valid for this chemical process at high temperatures.

However, at temperatures below 225 °C, the reaction is described by a different rate law that is second order with respect to NO₂:

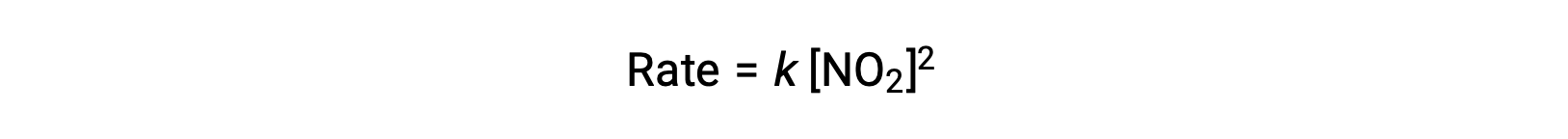
This rate law is not consistent with the single-step mechanism, but it is consistent with the following two-step mechanism:

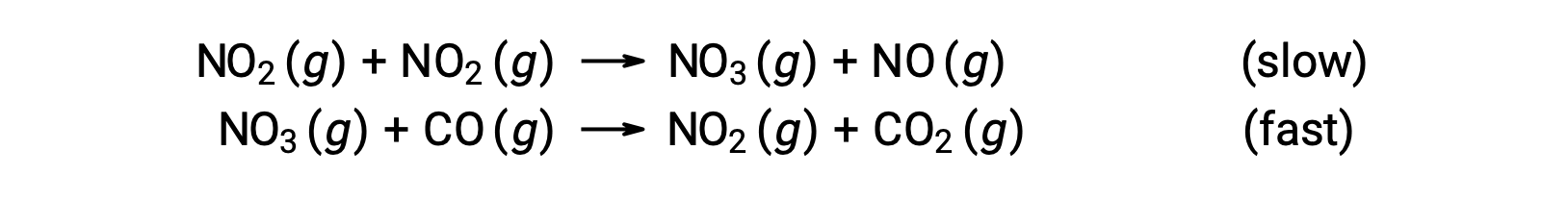
The rate-determining (slower) step gives a rate law showing second-order dependence on the NO₂ concentration, and the sum of the two elementary equations gives the overall net reaction.

In general, when the rate-determining (slower) step is the first step in the reaction mechanism, the rate law for the overall reaction is the same as the rate law for this step. However, when the rate-determining step is preceded by an elementary step involving a rapidly reversible reaction, the rate law for the overall reaction may be more difficult to derive, often due to the presence of reaction intermediates.

In such instances, the concept that a reversible reaction is at equilibrium when the rates of the forward and reverse processes are equal can be utilized.

For example, consider the reversible elementary reaction in which NO dimerizes to yield an intermediate species N₂O₂. When this reaction is at equilibrium:

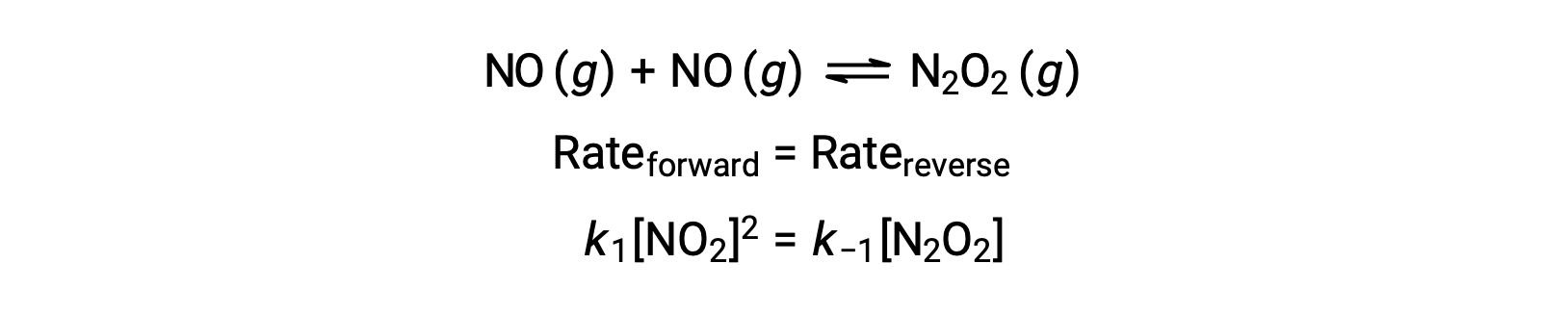
This expression may be rearranged to express the concentration of the intermediate in terms of the reactant NO:

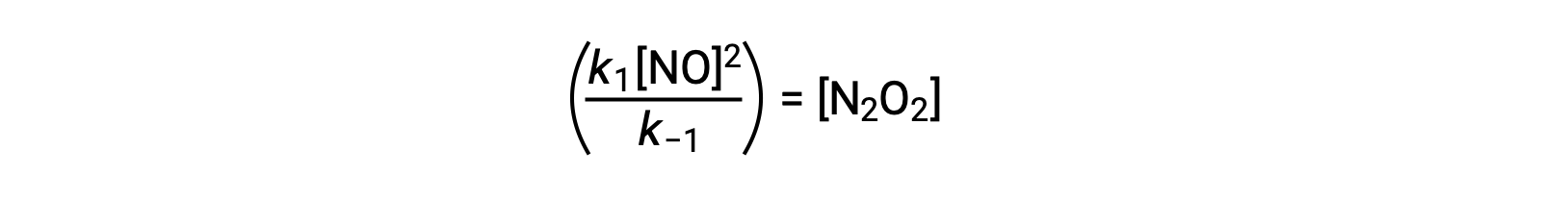
This approach can be utilized in formulating rate laws for overall reactions when reaction intermediates are present.

Example of Deriving the Rate Law from a Reaction Mechanism

Consider a reaction between nitrogen monoxide and molecular chlorine, for which a two-step mechanism is proposed as shown:

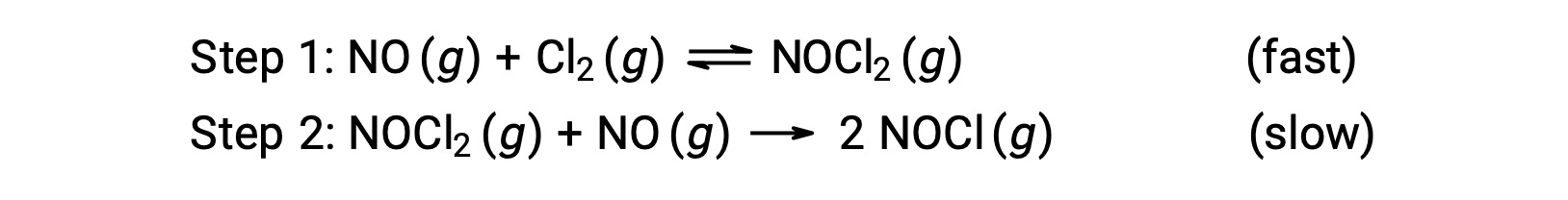
This mechanism can be used to derive the equation and predict the rate law for the overall reaction. Initially, by adding the two elementary reactions, the equation for the overall reaction is obtained.

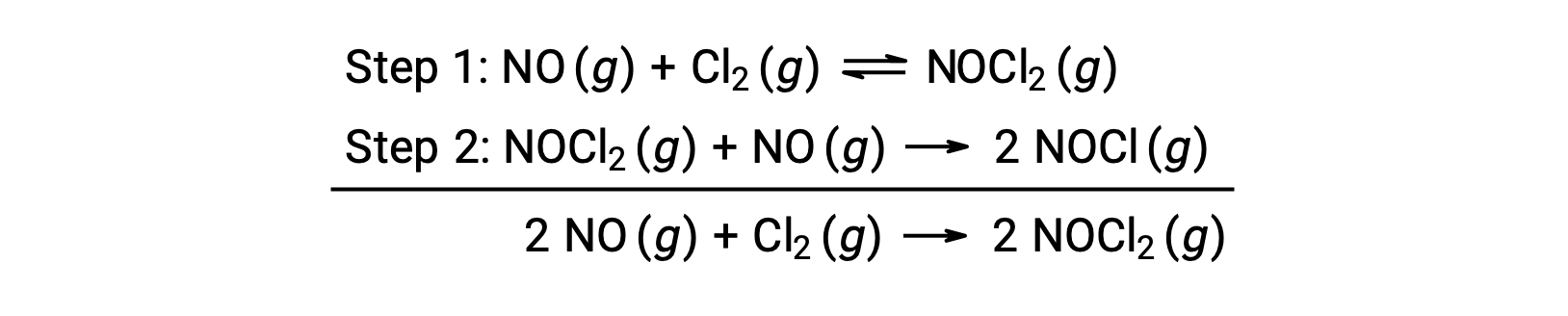
To derive a rate law from this mechanism, the rates laws for each of the two elementary steps are written:

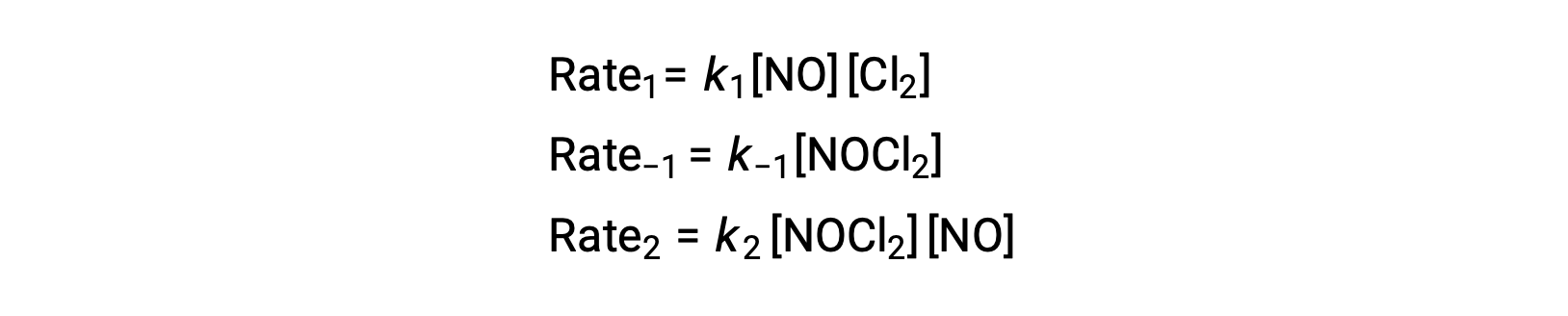
According to the proposed reaction mechanism Step 2 is the rate-determining step. Hence, the rate law for the overall reaction should be the same as the rate law for this elementary step. However, the rate law for Step 2 contains an intermediate species concentration, [NOCl₂]. To modify this, the rate law of the first elementary step is used to derive an expression for the intermediate concentration in terms of reactant concentrations.

Assuming Step 1 is at equilibrium;

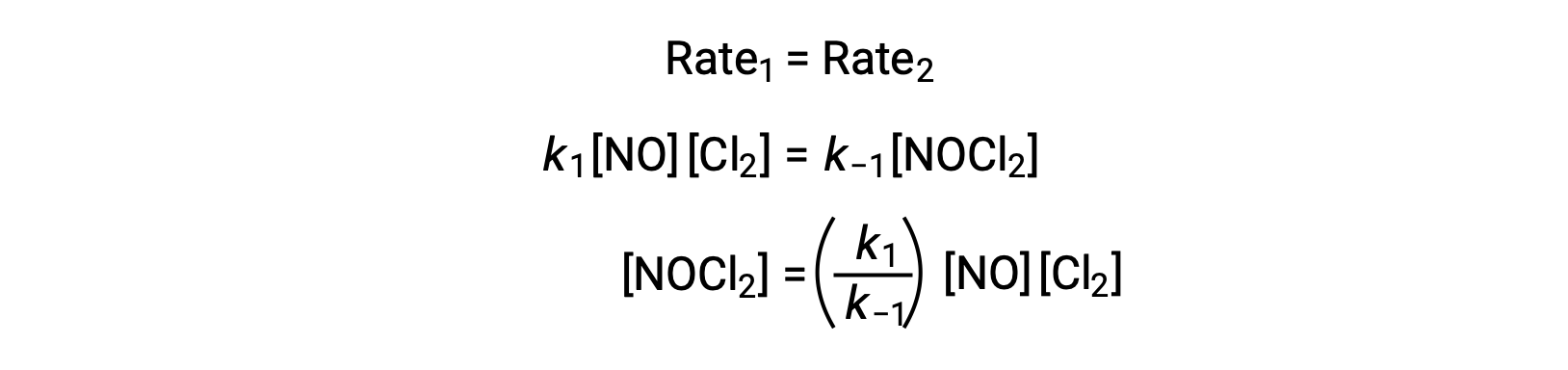
Substituting this expression into the rate law for Step 2 yields:

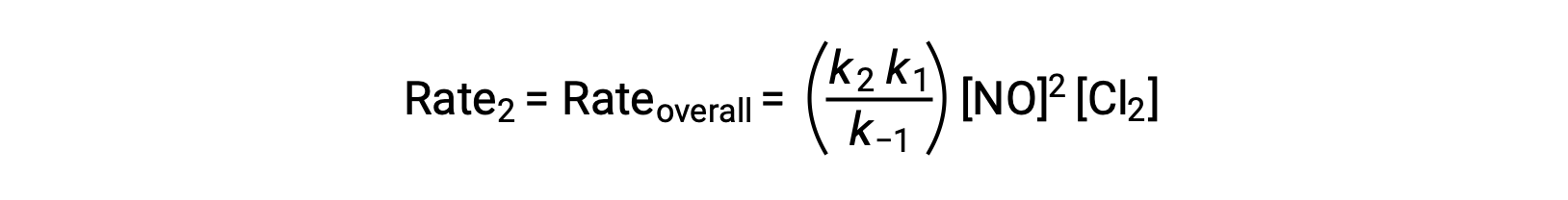
This text is adapted from Openstax, Chemistry 2e, Section 12.6: Reaction Mechanisms.

Procedure

Most chemical reactions proceed in a multistep reaction mechanism. But how is a reaction mechanism determined?

Reaction mechanisms are hypothesized based on their balanced chemical equations and experimentally determined rate laws of each elementary step.

Each step has a specific reaction rate, rate constant, and activation energy. The slowest step is called the rate-determining step and influences the net reaction rate. It can be used to verify the rate law for the overall reaction and to validate a proposed reaction mechanism.

Consider the decomposition of nitrous oxide to nitrogen and oxygen. The experimentally determined rate law does not correspond to the rate expression of a single-step reaction, which is corroborated by the observed presence of oxygen atoms—a reaction intermediate.

Hence, a reaction mechanism is proposed where all steps cumulate to give the overall reaction.

First, the rate constants indicate that the first step is the rate-limiting step. It is the slowest, and thus influences the overall reaction rate. A rate law proposed from this step can be set equal to the overall rate law.

This proposed rate-law, directly derived from the molecular concentration of the elementary reactant, matches the experimental rate-law and verifies the predicted reaction mechanism.

However, many reactions start with a fast initial step followed by a rate-determining step. How can reaction mechanisms be proposed in such cases?

Consider the formation of nitrosyl bromide. The experimental rate law is second-order for nitric oxide and first-order for molecular bromine.

The first step is a fast equilibrium step with equal forward and reverse reaction rates, followed by the second rate-determining step, which contains a reaction intermediate. Consequently, the proposed rate law will hold the intermediate.

Therefore, a straightforward comparison between the proposed rate law, containing the reaction intermediate with an unknown concentration, and the experimental rate law, accommodating the starting reactants, is difficult.

However, assuming that the first step is in equilibrium, the intermediate concentration can be set equal to the reactants' concentrations. Substituting this relationship into the proposed rate law, and combining the rate constants into an overall rate constant, generates an expression consistent with the experimental rate law.

Combining the elementary steps gives the overall balanced equation satisfying the second requirement for a reaction mechanism. Thus, the proposed two-step reaction mechanism of nitrosyl bromide formation is valid.