Overview
The Arrhenius equation relates the activation energy and the rate constant, k, for chemical reactions. In the Arrhenius equation, k = Ae−Ea/RT, R is the ideal gas constant, which has a value of 8.314 J/mol·K, T is the temperature on the kelvin scale, Ea is the activation energy in J/mole, e is the constant 2.7183, and A is a constant called the frequency factor, which is related to the frequency of collisions and the orientation of the reacting molecules.
The Arrhenius equation can be used to compute the activation energy of a reaction from experimental kinetic data. A convenient approach to determining the Ea for a reaction involves the measurement of k at two or more different temperatures. It uses a modified version of the Arrhenius equation that takes the form of a linear equation:
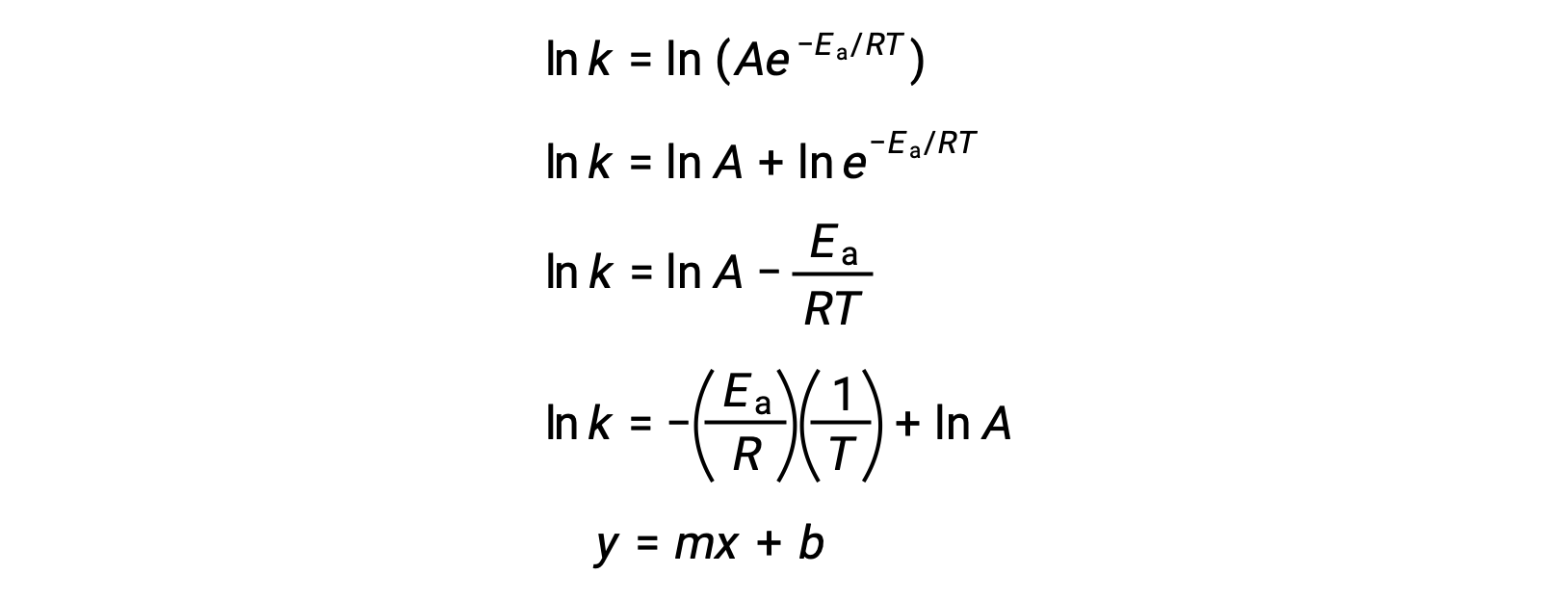
A plot of the ln k versus 1/T is linear with a slope equal to −Ea/R and y-intercept equal to ln A.
Consider the following reaction:
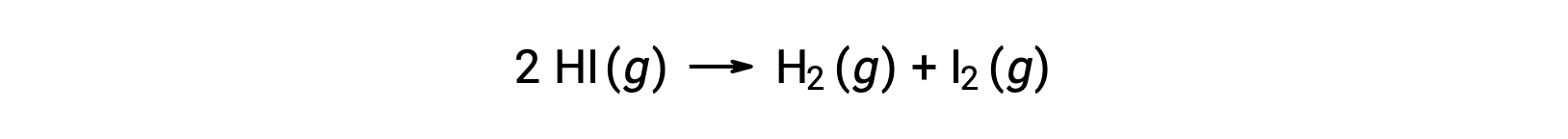
The activation energy of this reaction can be determined if the variation in the rate constant with temperature is known from the reaction kinetic data, as shown.
| Temperature (K) | Rate constant (L/mol/s) |
| 555 | 3.52 × 10–7 |
| 575 | 1.22 × 10–6 |
| 645 | 8.59 × 10–5 |
| 700 | 1.16 × 10–3 |
| 781 | 3.95 × 10–2 |
The provided data can be used to derive the values of the inverse of temperature (1/T) and the natural log of k (ln k).
| 1/T (K–1) | ln k |
| 1.80 × 10–3 | –14.860 |
| 1.74 × 10–3 | –13.617 |
| 1.55 × 10–3 | –9.362 |
| 1.43 × 10–3 | –6.759 |
| 1.28 × 10–3 | –3.231 |
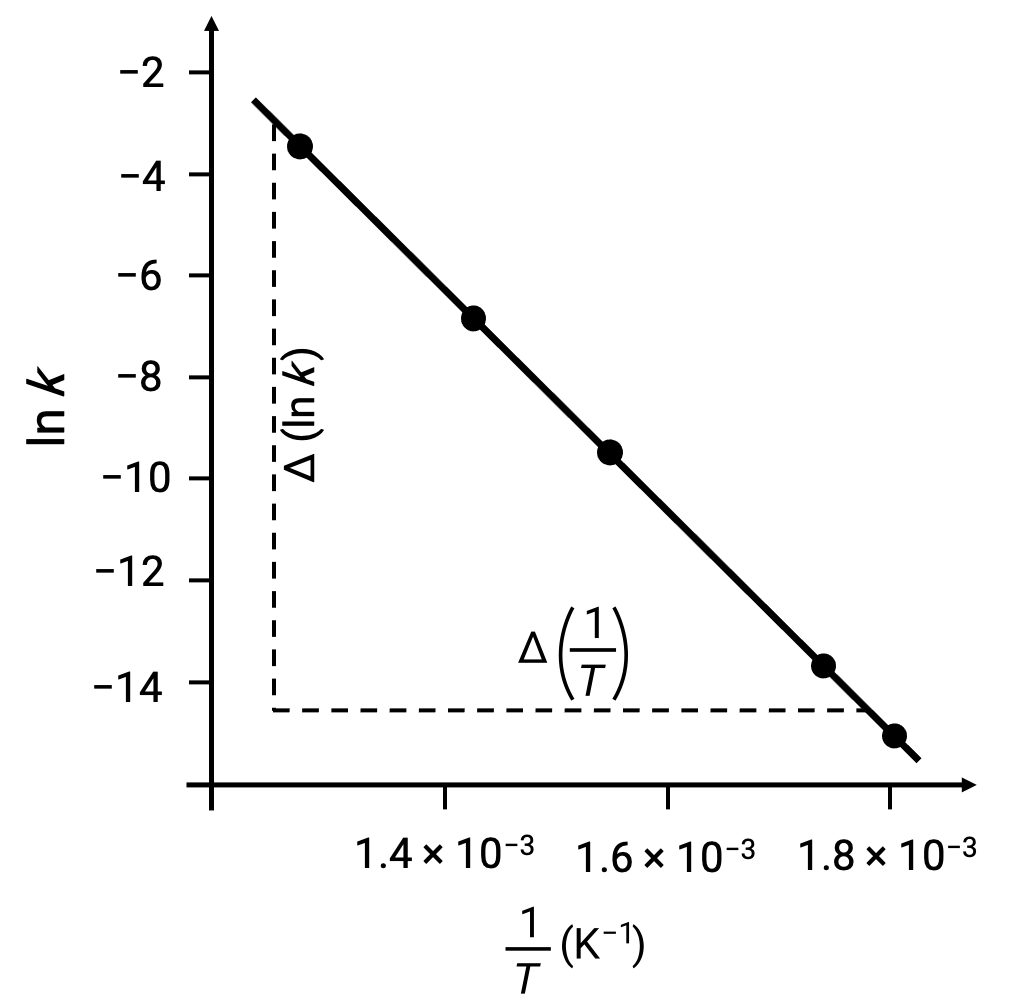
On plotting the derived data points with ln k versus 1/T, a line-graph exhibiting a linear relationship between ln k and 1/T is generated, as shown.
The slope of the line, which corresponds to the activation energy, can be estimated using any two of the experimental data pairs.

An alternative approach in deriving activation energy involves the utilization of the rate constant at two different temperatures. In this approach, the Arrhenius equation is rearranged to a convenient two-point form:
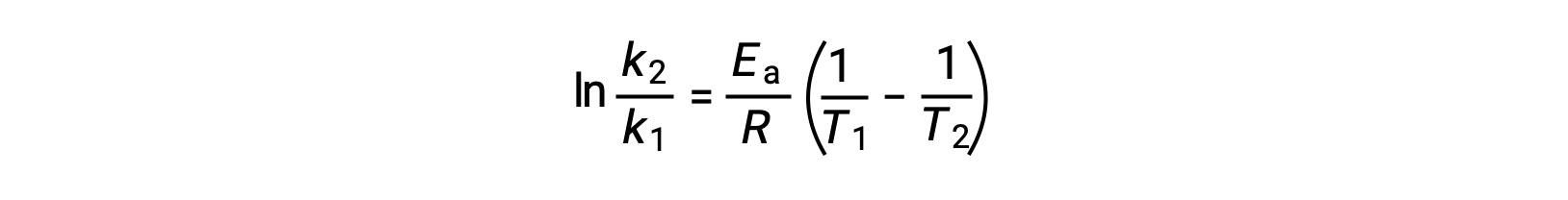
On rearranging the equation, an expression for the activation energy is generated.
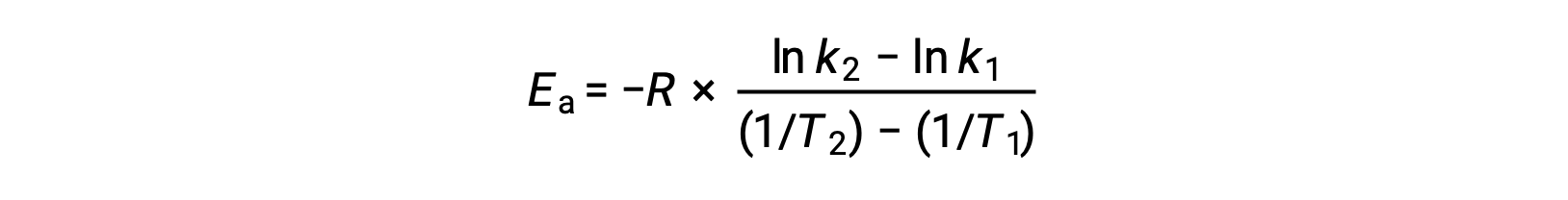
By substituting any two data pairs and further calculation yields the value for the activation energy in joules per mole or kilojoules per mole.
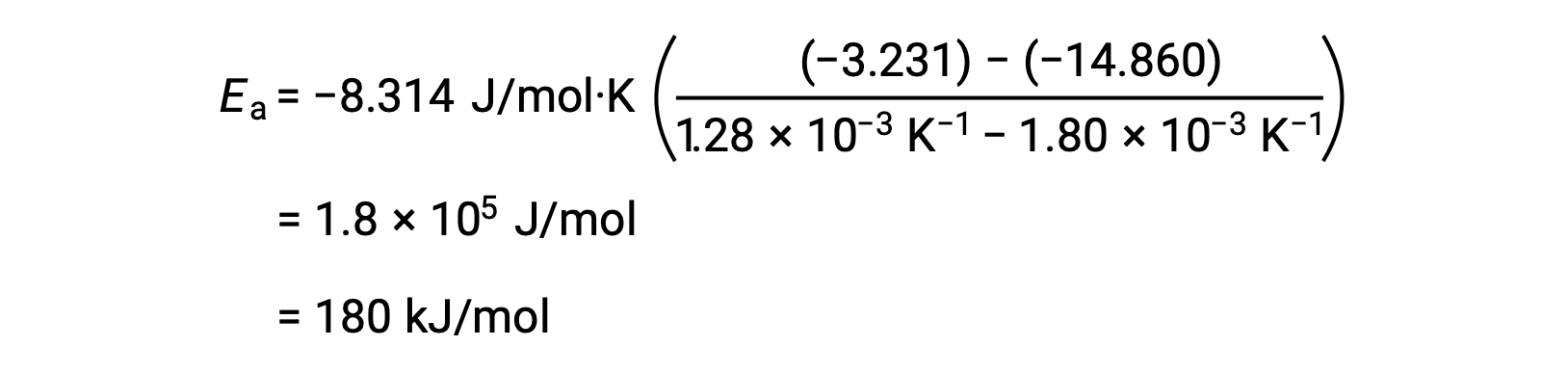
This alternative two-point approach yields the same result as the graphical approach. However, in practice, the graphical approach typically provides more reliable results while working with actual experimental data.
This text is adapted from Openstax, Chemistry 2e, Section 12.5: Collision Theory.
Procedure
The rate of a chemical reaction is highly sensitive to changes in temperature. This temperature dependence is mathematically explained using the Arrhenius equation; which expresses the relationship between the rate constant, the absolute temperature, the frequency factor, and the activation energy.
The activation energy and frequency factor can also be determined graphically by converting the Arrhenius equation into a non-exponential form.
Using the natural logarithms on both sides, an equation for a linear function is generated. The slope value corresponds to the negative value of activation energy over gas constant, and the y-intercept corresponds to the natural log of the frequency factor.
This equation can be used to generate a graph called the Arrhenius plot, in which the natural log of the rate constant is denoted as a function of the inverse of temperature in kelvin.
Kinetic data of experiments and reactions can be illustrated and analyzed using this Arrhenius plot. In this example, the graph yields a straight line. The slope value given in kelvin is set equal to the negative value of activation energy over R. After assigning the value for the gas constant and solving for the activation energy, a value of 93.1 kJ/mol is obtained.
Besides, the y-intercept of 26.8 is equal to the natural log of the frequency factor. Thus, solving for A gives the value of 4.36 × 1011 with the unit one-over-molarity-seconds — the same unit as the rate constant.
In cases of limited kinetic data or difficulties with graphical representation, a two-point form of the Arrhenius equation can be utilized to calculate the activation energy in a non-graphical manner.
In such cases, the non-exponential form of the Arrhenius equation is modified to include rate constants at two different temperatures.
Subsequent subtraction and rearrangement of the expression yield the two-point form of the Arrhenius equation, which is used to calculate the activation energy from experimentally-generated rate constants at two different temperatures. By substituting the values, the activation energy for this reaction is calculated to be 145 kJ/mol.