Overview
The half-life of a reaction (t1/2) is the time required for one-half of a given amount of reactant to be consumed. In each succeeding half-life, half of the remaining concentration of the reactant is consumed. For example, during the decomposition of hydrogen peroxide, during the first half-life (from 0.00 hours to 6.00 hours), the concentration of H2O2 decreases from 1.000 M to 0.500 M. During the second half-life (from 6.00 hours to 12.00 hours), the concentration decreases from 0.500 M to 0.250 M, while during the third half-life, it falls from 0.250 M to 0.125 M. Hence, during each successive period of 6.00 hours, the concentration of H2O2 decreases by half.
The half-life of a first-order reaction is independent of the concentration of the reactant. However, half-lives of reactions with other orders depend on the concentrations of the reactants.
Half-life of First-order Reactions
An equation relating the half-life of a first-order reaction to its rate constant may be derived from its integrated rate law:
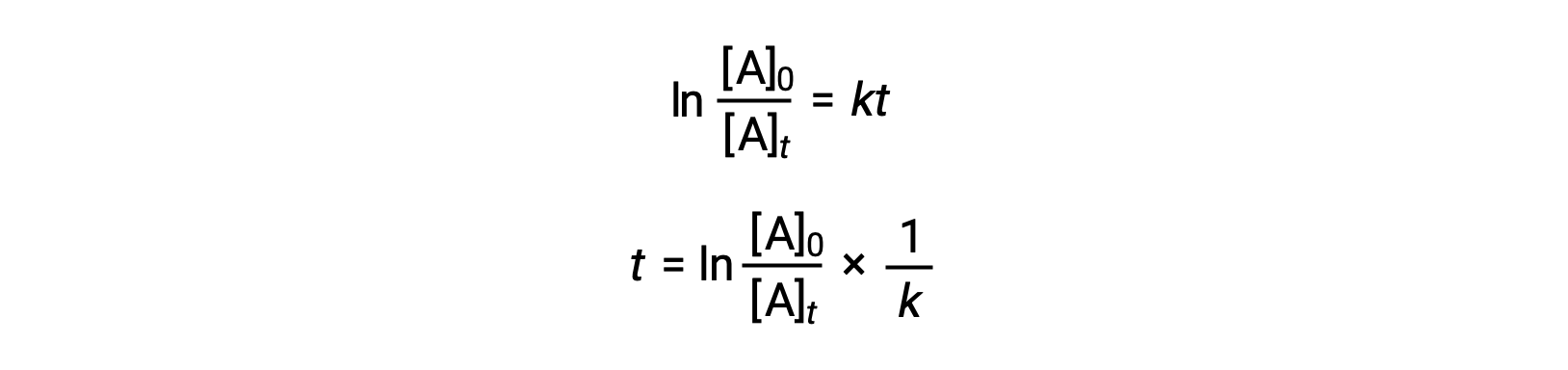
According to the definition of half-life, at time t1/2, the concentration of the reactant A is one-half of its initial concentration. Therefore; t = t1/2 and [A]t = ½ [A]0.
Substituting these terms into the rearranged integrated rate law and simplifying yields the equation for half-life:
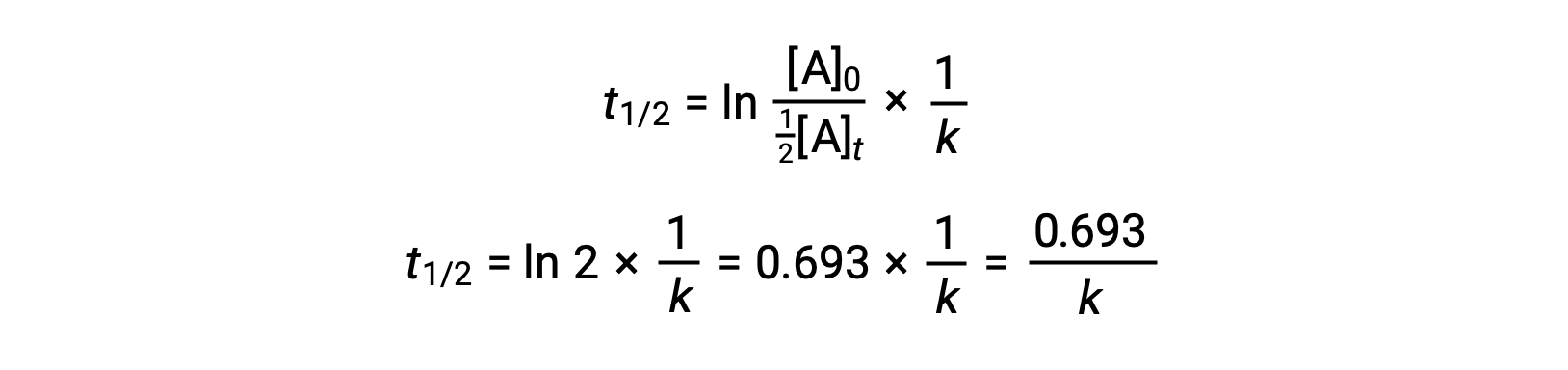
This half-life equation describes an expected inverse relationship between the half-life of the reaction and its rate constant, k. Faster reactions exhibit larger rate constants and correspondingly shorter half-lives, while slower reactions exhibit smaller rate constants and longer half-lives.
Half-life of Second-order Reactions
Following the same approach as for first-order reactions, an equation relating the half-life of a second-order reaction to its rate constant and initial concentration may be derived from its integrated rate law:
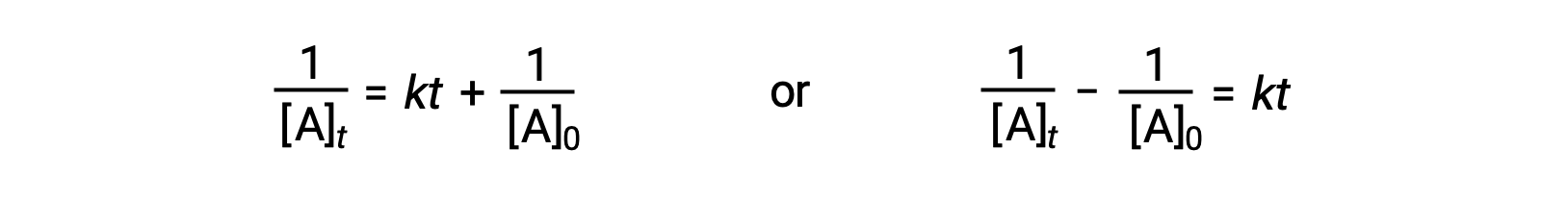
On substituting t = t1/2 and [A]t = ½[A]0, the integrated rate law is simplified:
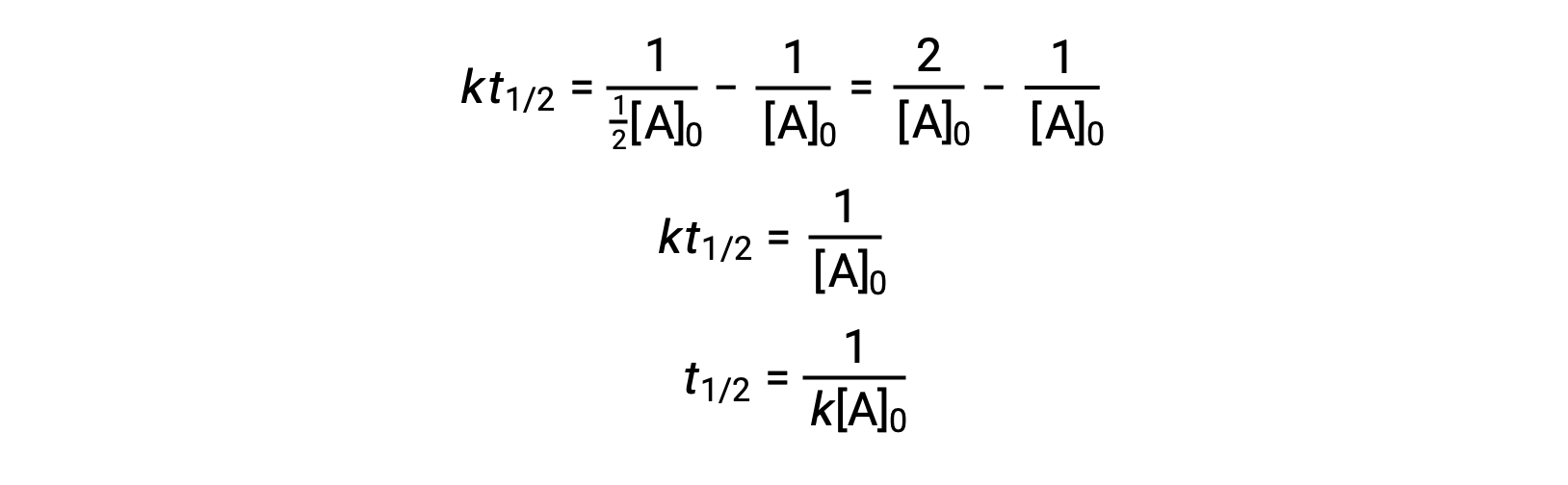
For a second-order reaction, t1/2 is inversely proportional to the concentration of the reactant, and the half-life increases as the reaction proceeds because the concentration of the reactant decreases. Unlike with first-order reactions, the rate constant of a second-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.
Half-life of Zero-order Reactions
An equation for zero-order half-life may be also be derived from its integrated rate law:
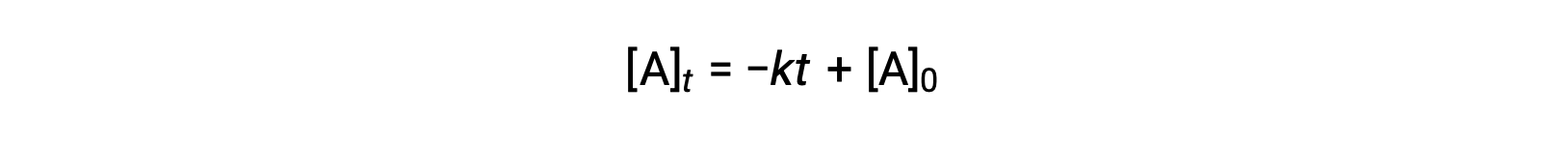
Substituting t = t1/2 and [A]t = ½ [A]0, in the zero-order integrated rate law yields:
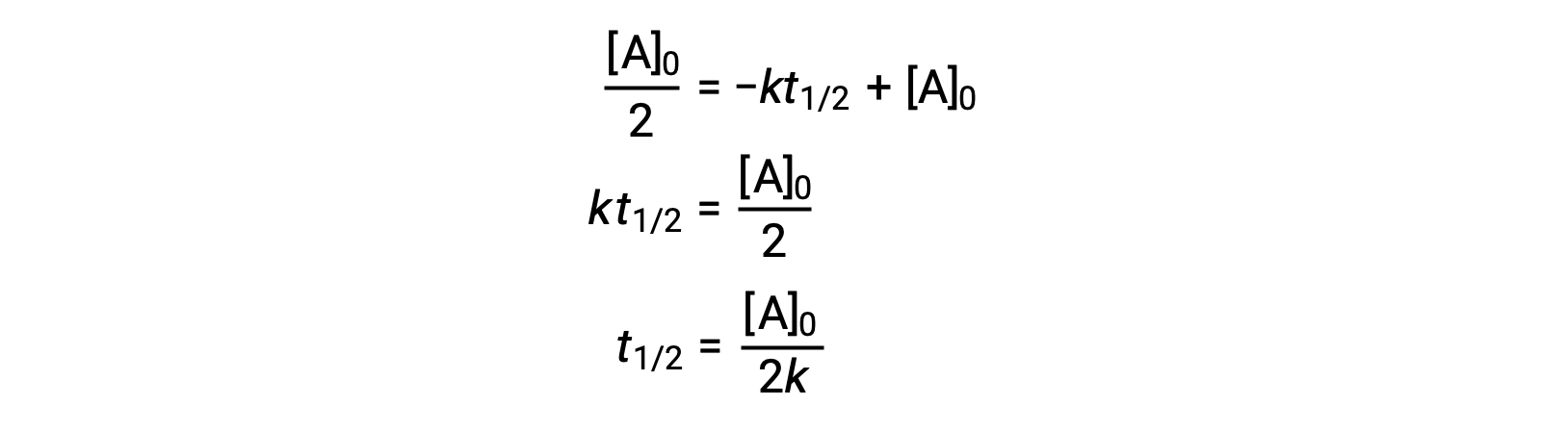
The half-life for a zero-order reaction is inversely proportional to its rate constant. However, the half-life of a zero-order reaction increases as the initial concentration increases.
This text is adapted from Openstax, Chemistry 2e, Section 12.4: Integrated Rate Laws.
Procedure
During a chemical reaction, the reactant’s concentration decreases over time. The time taken to reduce it to half of its initial quantity is called the half-life of the reaction, abbreviated as t1/2.
Consider the refrigerant trichlorofluoromethane, which depletes the ozone layer. Its atmospheric residence time is 45 years and it is banned in many countries. But how long does it take for the concentration to drop to 50%? To estimate a reactant’s concentration after an elapsed time, the half-life can be used.
The half-life differs for each reaction type. Depending on the reaction order, a general half-life expression can be derived from the integrated rate laws.
Consider the zero-order integrated rate law. At t1/2, the reactant concentration is half of its initial concentration. On substitution of these parameters, an expression for the half-life is formulated.
The formula shows that the half-life for a zero-order reaction is dependent on and directly proportional to the initial reactant concentration. As the reactant concentration declines, the half-life continues to get shorter.
For a first-order reaction, the integrated rate expression is modified by substituting the time as t1/2 and the reactant quantity as half of its initial concentration. On solving, the expression for t1/2 is determined to be a constant.
Thus, the half-life of a first-order reaction is derived to be independent of the initial reactant concentration. Regardless of the decrease in the reactant concentration, the half-life remains constant.
For a second-order reaction, the integrated rate expression is converted to t1/2 by substituting the time and reactant concentration parameters.
The half-lives of second-order reactions are inversely dependent on the initial reactant concentration. As the reactant concentration decreases, the t1/2 value increases; meaning, the half-life continues to get longer.
The half-life also helps to estimate the magnitude of the rate constant. It offers a relative comparison between different reaction rates; the shorter the half-life, the faster the reaction rate and vice-versa.
For instance, the radioactive isotope sodium-24, with a short half-life of 14.7 hours, exhibits a faster decay rate than cobalt-60, with a longer half-life of 5.3 years