Overview

Source: Laboratory of Dr. Neal Abrams — SUNY College of Environmental Science and Forestry

All chemical reactions have a specific rate defining the progress of reactants going to products. This rate can be influenced by temperature, concentration, and the physical properties of the reactants. The rate also includes the intermediates and transition states that are formed but are neither the reactant nor the product. The rate law defines the role of each reactant in a reaction and can be used to mathematically model the time required for a reaction to proceed. The general form of a rate equation is shown below:

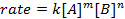
    Equation 1

where A and B are concentrations of different molecular species, m and n are reaction orders, and k is the rate constant. The rate of nearly every reaction changes over time as reactants are depleted, making effective collisions less likely to occur. The rate constant, however, is fixed for any single reaction at a given temperature. The reaction order illustrates the number of molecular species involved in a reaction. It is very important to know the rate law, including rate constant and reaction order, which can only be determined experimentally. In this experiment, we will explore one method for determining the rate law and use it to understand the progress of a chemical reaction.

Principles

Kinetics and Thermodynamics

All chemical reactions are governed by two factors, kinetics and thermodynamics. The thermodynamic factor is the difference in free energy released during a chemical reaction. This free energy, termed spontaneity, is a complex value arising from the enthalpy (heat) and entropy (disorder) within a chemical reaction. Kinetics refers to the rate of a chemical reaction and how fast the system reaches equilibrium. While kinetics can explain the speed of the reaction, thermodynamics yields information about its energetics. Simply stated, thermodynamics relates to stability and kinetics relates to reactivity.

Determining Rate

Rate is a time-based measurement, meaning it is constantly changing as a reaction proceeds. This can be represented using a differential rate law, expressing the change in concentration over a change in time. Experimentally, the differential rate law is difficult to use, so we can use calculus and represent the rate law as the integrated rate law by integrating the differential rate law. The integrated rate law represents the reaction concentrations at the start of the reaction and at a specified time interval. A table of order, rate law, and integrated rate law is shown below:

Table 1

Each order explains the dependence of reactant concentration on reaction rate. For example, a zeroth order rate law, rate = k, indicates that the rate is only dependent on the rate constant, not on reactant concentration. This is common in catalytic reactions where the catalyst is a solid and the surface area does not change during the reaction. A 1st order rate law shows that the rate is dependent on the concentration of one reactant, though other reactants may be present. A 2nd order rate law indicates that the rate is dependent on the concentration of two reactants in the reaction. Those reactants can be the same, i.e. rate = k[A]2, or different, rate = k[A][B]. Since the two concentrations are constantly changing, second order rate constants can be difficult to measure in the lab. Regardless of the order, using the integrated rate law simplifies data analysis by allowing for data plotting and applying a linear equation to fit the data. Since only one integrated rate law will fit the data, a reaction's rate constant and reaction order can be immediately identified.

A Kinetics Experiment

Determining the rate law begins with setting up a kinetics experiment for the chemical reaction. A kinetics experiment is carefully controlled so that measurements are made in timed intervals in order to determine the change in concentration of a species over time. That species can either be a reactant (decreasing concentration with time) or a product (increasing concentration with time). If multiple reactants are involved, it is also very important that the concentration of only one reactant changes with time. Increasing the concentration of the other reactants much higher than the reactant being studied makes it appear that the concentration of only one reactant changes during the experiment.

In this experiment, the catalytic decomposition of hydrogen peroxide over a platinum catalyst is explored. Since the platinum is a catalyst, only one species is involved which decomposes into two products according to the reaction below:

    2 H2O2(aq) → O2(g) + 2 H2O(l)

Because one of the products, O2, is a gas, the increase in pressure of the system over time can be measured and the Ideal Gas Law (PV = nRT) used to relate pressure to moles. Once that is done for several different concentrations of the reactant, the reaction order and rate law can be solved.

Procedure

1. Preparing H2O2 Dilutions

  1. Stock 3% hydrogen peroxide has a concentration of 0.882 M. Prepare 5 dilutions ranging from 0.882 M to 0.176 M (Table 1). Prepare these solutions volumetrically, but prepare them additively since the solute is very dilute and volumes of water are additive.
  2. Place the solutions in a constant temperature water bath or leave them on the bench top to equilibrate at room temperature. A temperature range of 20–25 °C (293–298 K) is good for this reaction.

Table 2
Table 1. H2O2 solutions used.

2. Preparing the Reaction Vessel

  1. To determine the volume of the reaction vessel, fill a large test tube to the top with water and insert a 1-hole rubber stopper into the test tube until tight and water pushes out the sides and through the top.
  2. Remove the stopper and pour the water into a graduated cylinder to determine the exact volume of the water. This is the total volume of the reaction vessel (test tube).

3. Measuring Oxygen Evolution

  1. Replace the water with 50 mL of the first hydrogen peroxide solution and place it back into the water bath. Once equilibrated, add the platinum-coated reaction disc and seal the system with a stopper connected to a gas pressure sensor. These discs are commonly used in contact lens cleaning systems.
  2. Once the pressure sensor is setup to acquire data at 2 points/s, run the experiment for 120 s. The Vernier gas pressure sensor, GPS-BTA, is recommended for this experiment.
  3. Bubbles should be observed as the peroxide is decomposed to oxygen gas and water. Release the pressure, dispose of the solution, rinse, and replace the solution with the next hydrogen peroxide solution. Repeat the gas pressure measurement until all solutions are tested.

4. Data Analysis

  1. Transfer all data files of pressure versus time to a spreadsheet program.
  2. Determining initial rates -assume that the concentration of hydrogen peroxide has not changed much during the short timeframe of the experiment. The data represent the initial linear region of the kinetics experiment.
    1. Determine slope by plotting pressure versus time and using a slope formula or linear regression. Plot the pressure in any common unit.
    2. The slope is the initial rate in units of pressureO2/s.
  3. Determining Reaction Order
    1. Because pressure of evolved O2 is directly proportional to the moles of decomposed H2O2, plotting the ln(initial rate) vs. ln[H2O2]0 yields a slope equivalent to the order of the reaction. The initial concentration of hydrogen peroxide, [H2O2]0, is what was used in each of the trials.
      1. The equation for the rate law is Equation 2. Taking the natural logarithm (ln) of the equation produces a linear equation Equation 3, where m, the slope, is the order of the reaction.
  1. Determining the Rate Constant, k
    1. For each trial, convert the rate, PO2/s, into units of atm/s if the rate is in a different unit such as torr/s.
    2. Because bubbles were evolved in aqueous solution, subtract the vapor pressure of water from the system pressure for each trial. The new rate reflects only the pressure due to oxygen evolution.
    3. Apply the Ideal Gas law to convert the rate from atm/s into moles/s in each trial.
      1. Rearrange PV = nRT to n = PV/RT. The s-1 unit remains unchanged. The volume is equivalent to the test tube volume minus the solution volume (50 mL).
    4. Use the balanced chemical reaction to convert from moles of oxygen produced to moles of hydrogen peroxide decomposed in each trial.
    5. Divide the moles of H2O2 by the volume of the solution, 0.050 L, to yield the molarity of H2O2 decomposed per second, [H2O2]/s.
    6. Because this experiment follows first-order kinetics, divide the rate, [H2O2]/s, by the original solution concentration for each trial, [H2O2]0, to yield a rate constant, k. This solution for the rate constant would vary slightly based on the order of the reaction previously determined.
    7. Average the rate constants for each trial together since the temperature is constant.

Results

Oxygen Evolution Data and Initial Rates

Figure 2
Figure 1. Pressure vs. time data for each trial at constant temperature. The slope is equivalent to the instantaneous rate of the reaction.

Reaction Order

  1. Data for five trials and graph with slope is tabulated below (Table 2, Figure 2). The slope of 0.9353 ≈ 1, is an integer value of the reaction order.

Table 3
Table 2. Results from 5 H2O2 trials.

Figure 1
Figure 2. Natural log plot of concentration vs. rate. The slope is equivalent to the order of the reaction.

Rate Constant, k

  1. Calculate the rate in mol O2/s using the Ideal Gas law by first subtracting out the vapor pressure of water at 294 K (temperature of the kinetics experiment), 18.7 torr.
  2. Calculate the rate constant by dividing the rate, [H2O2]/s by the initial concentration of [H2O2]0.

Table 4
Table 3. Calculation of the rate constant, k.

  1. The average rate constant, 2.25 x 10-4 s-1 indicates the reaction is first order based on the units. The rate law could be rewritten as: rate = 2.25 x 10-4 s-1[H2O2]0

Applications and Summary

While determining rate law variables can be involved mathematically, the methods are actually quite straightforward. As long as the disappearance of a reactant or appearance of a product can be measured, rate plots can used to calculate the rate constant. An extension of this method is frequently used to determine the activation energy of a reaction, Ea, by measuring the rate and calculating the rate constant at a variety of temperatures. This method involves using the Arrhenius equation, k = Ae(-Ea/RT). Combining the rate law, including reaction order, with the activation energy of a reaction provides a full kinetic profile for how fast (or slow) a reaction progresses and provides real-world information on how factors like temperature and concentration can affect that reaction.

Chemical kinetics find applications in industries and fields as varied as pharmaceuticals, nuclear safety, environmental remediation, and sunscreens. For example, a certain drug may have a very large rate constant, meaning it decays very quickly in the body. This affects usage, dosing, and delivery method. With respect to nuclear science, radioactivity follows first-order kinetics, meaning that the time required for nuclear material to decay to a safe level is very well characterized. Measurements would be very similar to the method presented here and could also be applied to the decay of many environmental pollutants. Similarly, sunscreens also decay with known kinetic profiles allowing manufacturers to inform consumers how soon the sunscreen needs to be applied to maintain safe levels.