Overview

The free energy change for a process may be viewed as a measure of its driving force. A negative value for ΔG represents a driving force for the process in the forward direction, while a positive value represents a driving force for the process in the reverse direction. When ΔG_rxn is zero, the forward and reverse driving forces are equal, and the process occurs in both directions at the same rate (the system is at equilibrium).

Recall that Q is the numerical value of the mass action expression for the system, and its value may be used to identify the direction in which a reaction will proceed in order to achieve equilibrium. When Q is lesser than the equilibrium constant, K, the reaction will proceed in the forward direction until equilibrium is reached and Q = K. Conversely, if Q > K, the process will proceed in the reverse direction until equilibrium is achieved.

The free energy change for a process taking place with reactants and products present under nonstandard conditions (pressures other than 1 bar; concentrations other than 1 M) is related to the standard free energy change according to this equation:

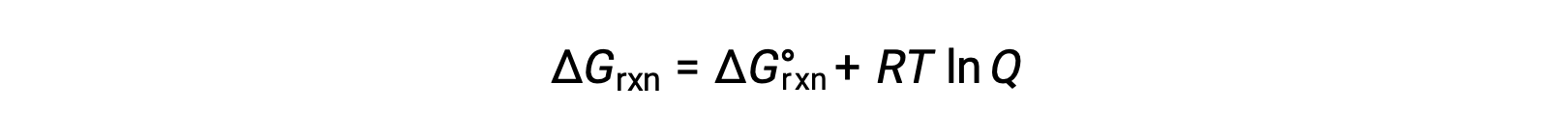
R is the gas constant (8.314 J/K mol), T is the kelvin or absolute temperature, and Q is the reaction quotient. For gas-phase equilibria, the pressure-based reaction quotient, Q_p, is used. The concentration-based reaction quotient, Q_c, is used for condensed phase equilibria. This equation may be used to predict the spontaneity of a process under any given set of conditions

For a system at equilibrium, Q = K and ΔG_rxn = 0, and the previous equation may be written as

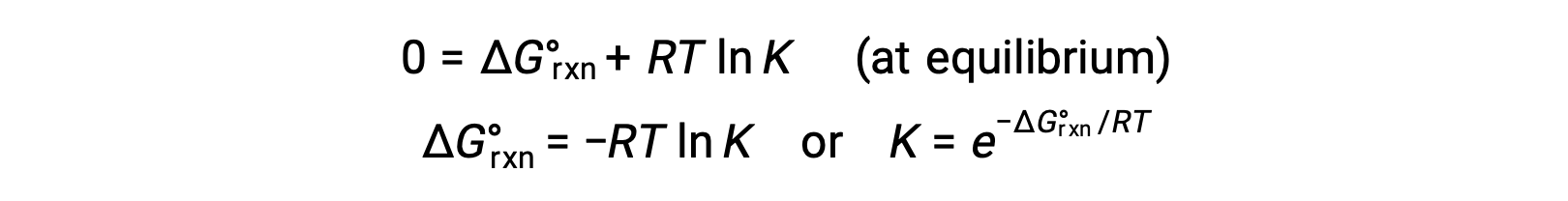
This form of the equation provides a useful link between these two essential thermodynamic properties, and it can be used to derive equilibrium constants from standard free energy changes and vice versa. The relations between standard free energy changes and equilibrium constants are summarized below.

If K > 1, ΔGº_rxn < 0 and the products are more abundant in the reaction mixture.

If K < 1, ΔGº_rxn > 0 and the reactants are more abundant in the reaction mixture.

 K = 1, ΔGº_rxn = 0 and the reactants and products are comparably abundant in the reaction mixture.

The standard free energy for a reaction change depends on temperature:

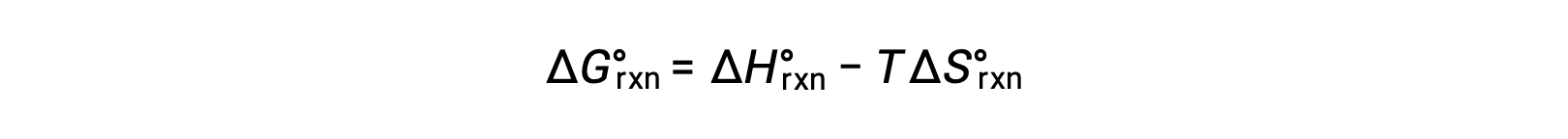
The standard free energy change for a reaction is related to the equilibrium constant for a reaction:

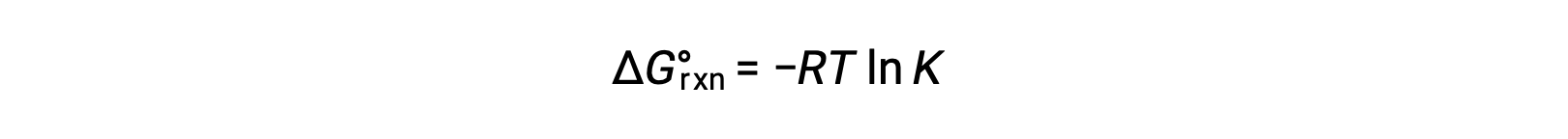
Combining the two expressions:

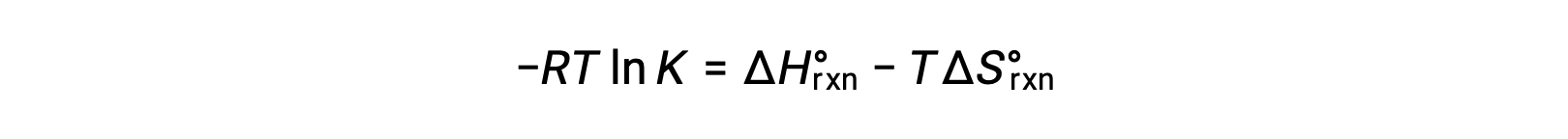
Dividing both sides by RT gives

Rearranging gives

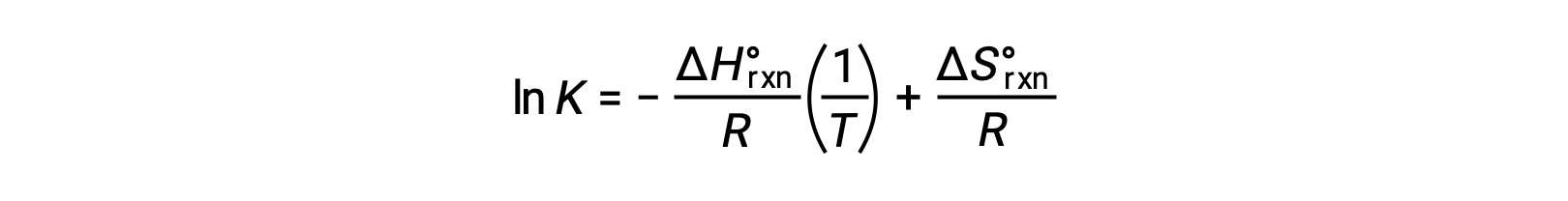
The equation takes the form of a straight line y = mx + b. A plot of ln K plotted against 1/T yields a straight line with a slope of −ΔHº_rxn/R and a y-intercept of ΔSº_rxn/R. The equation can also be expressed in a two-point form:

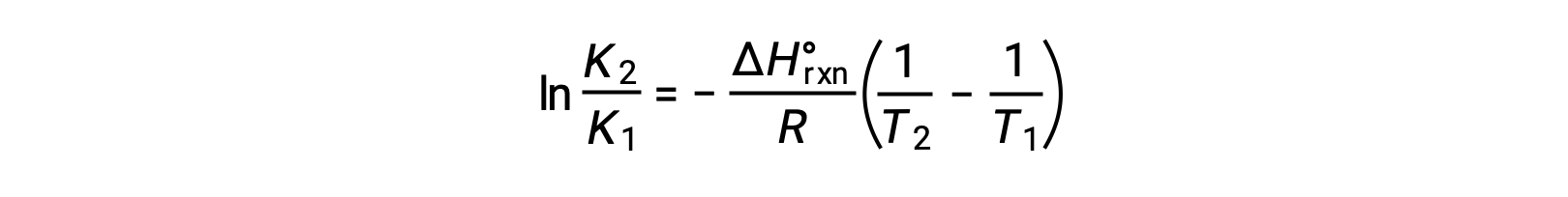
This text is adapted from Openstax, Chemistry 2e, Chapter 16.4: Free Energy.

Procedure

Both the equilibrium constant and the standard free energy change can be used to determine whether a reaction is product or reactant favored.

For any reaction mixture composition, the ΔG for the reaction is the sum of the standard free energy and RT times the natural log of the reaction quotient.

When the reactants and products are at equilibrium, the free energy change is zero, and the reaction quotient equals the equilibrium constant. So the standard free energy change equals −RT ln K.

If ΔG naught is less than zero, ln K is positive, meaning K is greater than 1. In this case, product formation is favored at equilibrium. The larger the equilibrium constant, the more negative the free energy. 

Take, for example, the breakdown of dinitrogen tetroxide at 298 kelvin, in which K is 1.34 × 10¹⁷. 

Substituting the known values into the equation, the standard free energy for the reaction equals −98 kJ/mole, and product formation is favored.

Conversely, if ΔG naught is greater than zero, ln K is negative, meaning K is less than 1 and the reverse direction of the reaction is favored.

Consider the breakdown of sulfur trioxide gas at 298 kelvin, which has a ΔG naught of 141.6 kJ/mole.

The equation can be rearranged so ln K equals negative ΔG over RT.

Substituting the known values into the equation, and raising e to the power of the result, K is very small—indicating that the reactant is favored.

Notably, if the temperature varies, the equilibrium constant will also change.

The temperature dependence of the equilibrium constant can be derived from the equation that directly relates K to the ΔG naught for the reaction.

The ΔG naught can be replaced by the standard enthalpy minus temperature times the standard entropy. Dividing both sides by negative RT yields ln K equals negative ΔH over RT plus ΔS over R.

This equation is in the form of a straight line where the natural log of K can be plotted against the inverse of the temperature in kelvins with a slope of negative ΔH over R and a y-intercept of ΔS over R.

If the values of K are measured at two slightly different temperatures, then this graph can also be used to calculate the change in enthalpy, assuming it remains constant over a limited temperature range.