Overview
Entropy is a state function, so the standard entropy change for a chemical reaction (ΔS°rxn) can be calculated from the difference in standard entropy between the products and the reactants.
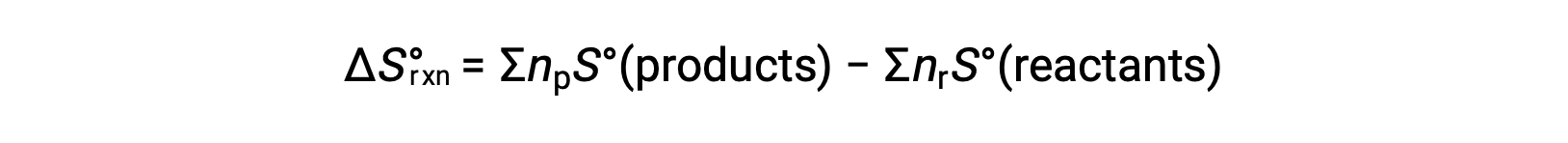
where np and nr represent the stoichiometric coefficients in the balanced equation of the products and reactants, respectively.
For example, ΔS°rxn for the following reaction at room temperature
is computed as follows:
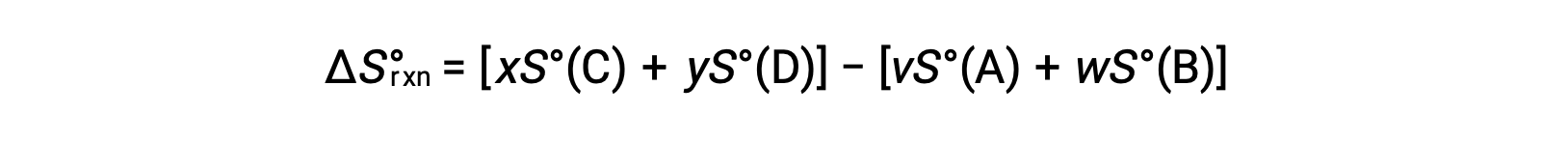
A partial listing of standard entropies is provided in the table.
| Substance | S° (J/mol·K) |
| C (s, graphite) | 5.740 |
| C (s, diamond) | 2.38 |
| CO (g) | 197.7 |
| CO2 (g) | 213.8 |
| CH4 (g) | 186.3 |
| C2H4 (g) | 219.5 |
| C2H6 (g) | 229.5 |
| CH3OH (l) | 126.8 |
| C2H5OH (l) | 160.7 |
| H2 (g) | 130.57 |
| H (g) | 114.6 |
| H2O (g) | 188.71 |
| H2O (l) | 69.91 |
| HCI (g) | 186.8 |
| H2S (g) | 205.7 |
| O2 (g) | 205.03 |
Determination of ΔS°
Consider the condensation of water, in which 1 mole of gaseous H2O changes into 1 mole of liquid H2O.
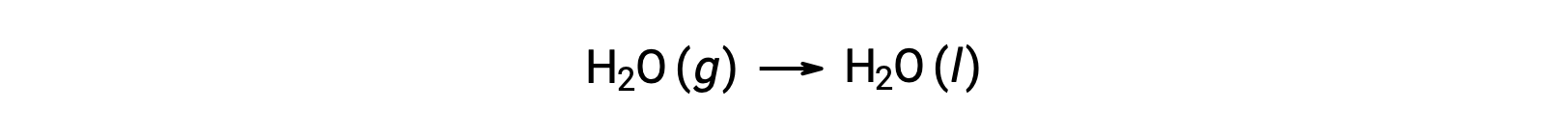
The standard entropy changes for the reaction, ΔS°rxn is calculated using the standard molar entropies and stoichiometric coefficients.
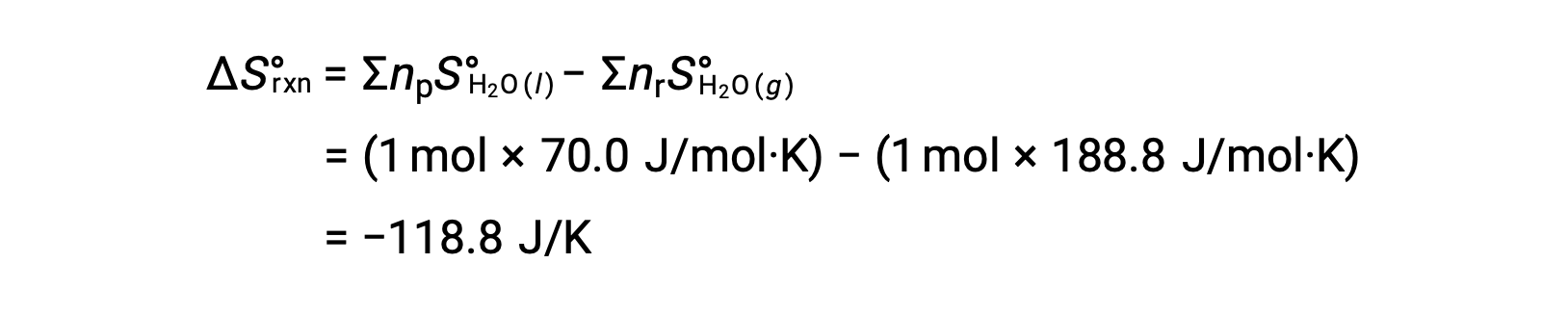
The value for ΔS°rxn is negative, as expected for this phase transition (condensation).
As a second example, consider the combustion of methanol, CH3OH:
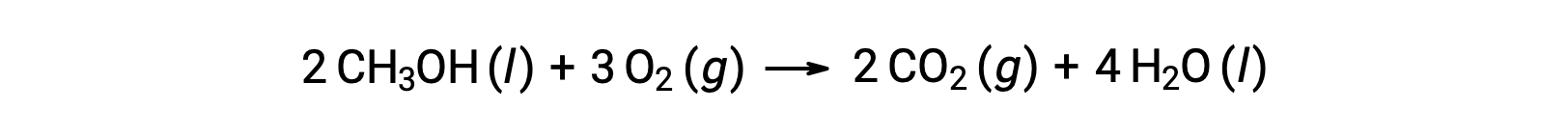
The same procedure is followed to calculate the standard entropy change of the reaction:
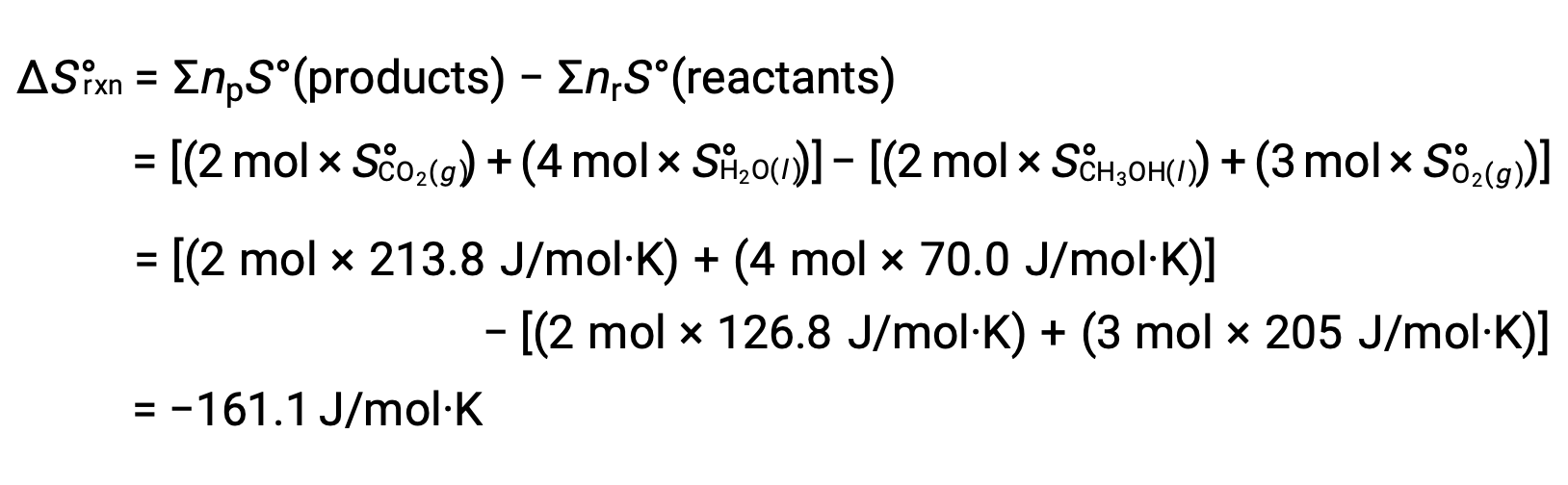
This text is adapted from Openstax, Chemistry 2e, Chapter 16.2: The Second and Third Law of Thermodynamics.
Procedure
Enthalpy changes associated with a chemical reaction can be measured with a calorimeter, but the entropy change associated with a reaction cannot be directly measured.
Entropy is a state function, which means that the change in entropy depends solely on the initial and final states of a system. So, like enthalpy changes, entropy changes can be from calculated reference tables of standard molar entropies.
For a reaction occurring under standard conditions, the associated entropy change is determined by the difference between the sum of the standard molar entropies of the products multiplied by their stoichiometric coefficients and the sum of the standard molar entropies of the reactants multiplied by their stoichiometric coefficients.
Consider the combustion of ethylene under standard conditions, where 1 mole of ethylene gas reacts with 3 moles of oxygen gas to produce 2 moles of carbon dioxide gas and 2 moles of water.
The standard entropy change for the reaction equals the sum of 2 times the standard entropy of carbon dioxide gas and 2 times the standard entropy of water, minus the sum of the standard entropy of ethylene gas and 3 times the standard entropy of oxygen.
Note that, unlike standard enthalpies of formation of elements, which are zero, standard molar entropies of all substances are greater than zero at 298 K.
Substituting the values for molar entropies of reactants and products from the reference table yields [(2 × 213.8) + (2 × 70.0)] − [(219.5 + 3) × (205.3)]. The net entropy of the products equals 567.6 J/K, and the net entropy of the reactants is 835.4 J/K.
The difference between the products and the reactants equals negative 268 J/K for the standard entropy change of the combustion of ethylene. The negative value indicates there is a decrease in entropy.
Even without calculating the exact entropy change, the decrease in entropy can be predicted by examining the reaction. Recall that gases are more disordered than liquids.
There are more moles of gas in the reactants, 4 moles of gas (with 1 mole of ethylene and 3 moles of oxygen) compared to the products (only 2 moles of carbon dioxide gas), while the other product is a liquid.
Thus, in this reaction, the reactants are more disordered than the products. Therefore, entropy decreases as the reaction proceeds.