Overview

Thus far, the ideal gas law, PV = nRT, has been applied to a variety of different types of problems, ranging from reaction stoichiometry and empirical and molecular formula problems to determining the density and molar mass of a gas. However, the behavior of a gas is often non-ideal, meaning that the observed relationships between its pressure, volume, and temperature are not accurately described by the gas laws. 

According to kinetic molecular theory, particles of an ideal gas do not exhibit attractive or repulsive forces on one another. They are assumed to have a negligible volume compared with that of the container. At room temperature and 1 atm or less, gases follow the ideal behavior, as implied by the ideal gas equation.

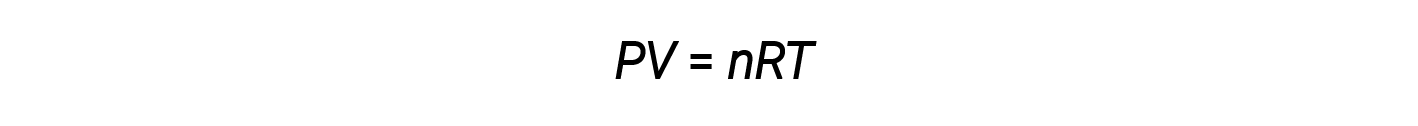
At higher pressures or lower temperatures, however, deviations from the ideal gas law occur, meaning that the observed relationships between its pressure, volume, and temperature are not accurately followed.

Rearranging the ideal gas equation to solve for n gives:

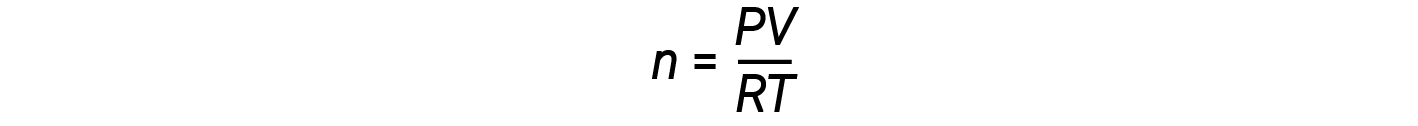
For 1 mole of an ideal gas, the ratio PV/RT = 1, regardless of pressure. Any deviation of this ratio from one is an indication of non-ideal behavior.

The ideal gas law does not describe gas behavior well at relatively high pressures. Meaning, the ratio equals 1 only at low pressures. But as the pressure rises, PV/RT begins to deviate from 1, and the deviations are not uniform. At high pressures, the deviation from ideal behavior is large and different for each gas. Real gases, in other words, do not behave ideally at high pressure. At lower pressures (usually below 10 atm), however, the deviation from ideal behavior is small, and we can use the ideal-gas equation.

Particles of a hypothetical ideal gas have no significant volume and do not attract or repel each other. In general, real gases approximate this behavior at relatively low pressures and high temperatures. However, at high pressures, the molecules of a gas are crowded closer together, and the amount of empty space between the molecules is reduced. At these higher pressures, the volume of the gas molecules themselves becomes appreciable relative to the total volume occupied by the gas. The gas, therefore, becomes less compressible at these high pressures, and although its volume continues to decrease with increasing pressure, this decrease is not proportional as predicted by Boyle’s law.

At relatively low pressures, gas molecules have practically no attraction for one another because they are (on average) so far apart, and they behave almost like particles of an ideal gas. At higher pressures, however, the force of attraction is also no longer insignificant. This force pulls the molecules a little closer together, slightly decreasing the pressure (if the volume is constant) or decreasing the volume (at constant pressure). This change is more pronounced at low temperatures because the molecules have lower KE relative to the attractive forces, and so they are less effective in overcoming these attractions after colliding with one another.

There are several different equations that better approximate gas behavior than does the ideal gas law. The first, and simplest of these, was developed by the Dutch scientist Johannes van der Waals in 1879. The van der Waals equation improves upon the ideal gas law by adding two terms: one to account for the volume of the gas molecules and another for the attractive forces between them.

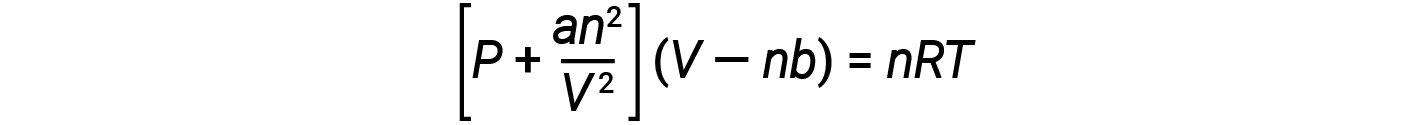
The constant a corresponds to the strength of the attraction between molecules of a particular gas, and the constant b corresponds to the size of the molecules of a particular gas. The “correction” to the pressure term in the ideal gas law is an²/V², and the “correction” to the volume is nb. Note that when V is relatively large and n is relatively small, both of these correction terms become negligible, and the van der Waals equation reduces to the ideal gas law, PV = nRT. Such a condition corresponds to a gas in which a relatively low number of molecules is occupying a relatively large volume, that is, a gas at relatively low pressure.

At low pressures, the correction for intermolecular attraction, a, is more important than the one for molecular volume, b. At high pressures and small volumes, the correction for the volume of the molecules becomes important because the molecules themselves are incompressible and constitute an appreciable fraction of the total volume. At some intermediate pressure, the two corrections have opposing influences, and the gas appears to follow the relationship given by PV = nRT over a small range of pressures.

Strictly speaking, the ideal gas equation functions well when intermolecular attractions between gas molecules are negligible, and the gas molecules themselves do not occupy an appreciable part of the whole volume. These criteria are satisfied under conditions of low pressure and high temperature. Under such conditions, the gas is said to behave ideally, and deviations from the gas laws are small enough that they may be disregarded — this is, however, very often not the case.

This text is adapted from Openstax, Chemistry 2e, Section 9.2: Non-ideal Gas Behavior.

Procedure

Ideal gases follow the relation PV over nRT equals one. Recall Boyle’s law, which states that when the amount and temperature of a gas are held constant, increasing the pressure will invariably decrease the volume to maintain a constant ratio. 

But when that ratio is plotted as a function of pressure for one mole of several real gases, it equals the ideal value “one” only at low pressures. As the pressure increases, the curves deviate significantly from ideality. 

At low pressures, the combined volume of gas particles is negligible relative to the container volume — like a pea inside a basketball. Therefore, the volume available to ideal gas particles equals the total container volume.

At higher pressures, the gas density is much greater. Thus, the combined volume of the gas particles becomes significant — like a pea inside a ping-pong ball. 

Therefore, the assumption of the kinetic molecular theory that gas particles occupy negligible volume is invalid at high pressures.

The volume occupied by a real gas is greater than the volume available to its particles, which is the volume it would occupy in an ideal case, by nb, where b is an experimentally determined constant that depends on the gas and has units of L/mol. 

Deducting nb adjusts the volume of a real gas downward to that available to its particles, which is equivalent to the ideal volume. 

Another assumption of the kinetic molecular theory — that intermolecular forces between gas molecules are negligible — is valid only under high-temperature and low-pressure conditions.

Typically, gases exert very weak attractive forces. Under low-pressure conditions, the gas particles are separated by large distances and, therefore, do not perceive the attractive forces of other particles.

Similarly, under high-temperature conditions, the particles have high kinetic energies relative to the attractive forces and move very quickly. When particles collide, they bounce off each other because the high kinetic energy overcomes the small attractive forces.

However, when the gas is at higher pressures, the particle density is greater. The particles are, therefore, separated by shorter distances, and the likelihood that they will interact thereby increases. The attractive forces between the particles accordingly become more significant at high pressures. 

This is more evident as the temperature is lowered. The kinetic energy of the particles decreases, and they move more slowly. When intermolecular attraction becomes significant, particles are increasingly likely to ‘stick’ to each other upon colliding. 

As gas particles spend more time interacting with neighboring particles, the frequency of collisions with the container surface decreases.

Consequently, the pressure exerted by a real gas is lower than that of an ideal gas by an²/V². Here, a is an experimentally determined constant that depends on the gas and has units of L²·atm/mol², and V is the real volume.

Adding this term adjusts the real pressure upward to that exerted by an ideal gas. The modified equation with the pressure and volume correction factors is called the van der Waals equation for non-ideal or real gases.